Тригонометрические тождества примеры доказательства. Старт в науке. История развития тригонометрии
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве
вида ![]() . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства
. Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства  и
и ![]() следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и ![]() сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть,
сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, ![]() , а котангенс есть отношение абсциссы к ординате, то есть,
, а котангенс есть отношение абсциссы к ординате, то есть, ![]() .
.
Благодаря такой очевидности тождеств и ![]() часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и ![]() имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула
имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула ![]() - для всех , отличных от , где z
- любое .
- для всех , отличных от , где z
- любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида ![]() . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
. Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы ![]() очень просто. По определению и , откуда
очень просто. По определению и , откуда  . Можно было доказательство провести и немного иначе. Так как и
. Можно было доказательство провести и немного иначе. Так как и ![]() , то
, то  .
.
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Тригонометрические тождества - это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
\[ \sin^{2}\alpha + \cos^{2} \alpha = 1 \]
\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \dfrac{\cos \alpha}{\sin \alpha} \]
\[ tg \alpha \cdot ctg \alpha = 1 \]
Зависимость между синусом и косинусом
\[ \sin^{2} \alpha+\cos^{2} \alpha=1 \]
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \]
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой \(\dfrac{y}{x}=\dfrac{\sin \alpha}{\cos \alpha} \) , а отношение \(\dfrac{x}{y}=\dfrac{\cos \alpha}{\sin \alpha} \) - будет являться котангенсом.
Добавим, что только для таких углов \(\alpha \) , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , .
Например: \(tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} \) является справедливой для углов \(\alpha \) , которые отличны от \(\dfrac{\pi}{2}+\pi z \) , а \(ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \) - для угла \(\alpha \) , отличного от \(\pi z \) , \(z \) - является целым числом.
Зависимость между тангенсом и котангенсом
\[ tg \alpha \cdot ctg \alpha=1 \]
Данное тождество справедливо только для таких углов \(\alpha \) , которые отличны от \(\dfrac{\pi}{2} z \) . Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что \(tg \alpha = \dfrac{y}{x} \) , а \(ctg \alpha=\dfrac{x}{y} \) . Отсюда следует, что \(tg \alpha \cdot ctg \alpha = \dfrac{y}{x} \cdot \dfrac{x}{y}=1 \) . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Зависимости между тангенсом и косинусом, котангенсом и синусом
\(tg^{2} \alpha + 1=\dfrac{1}{\cos^{2} \alpha} \) - сумма квадрата тангенса угла \(\alpha \) и \(\alpha \) , отличных от \(\dfrac{\pi}{2}+ \pi z \) .
\(1+ctg^{2} \alpha=\dfrac{1}{\sin^{2}\alpha} \) - сумма \(\alpha \) , равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \(\alpha \) , отличного от \(\pi z \) .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX! "Тригонометрические тождества". 10-й класс
“Математическая истина, независимо
от того, в Париже или в Тулузе, одна и та же”
Б. Паскаль
Тип урока: Урок формирования умений и навыков.
Урок общеметодологической направленности.
Деятельностная цель : формирование способности учащихся к новому способу действия, связанному с построением структуры изученных понятий и алгоритмов.
Цели урока:
дидактическая : научить применять полученные ранее знания, умения и навыки для упрощения выражений и доказательства тригонометрических тождеств.
развивающая: развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи, вырабатывать умение анализировать и сравнивать.
воспитательная: показать, что математические понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи, продолжить формирование эстетических навыков при оформлении записей, навыков контроля и самоконтроля.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sinα, cosα, tgα, ctgα,соотношение sin 2 α+ cos 2 α =1 и т.д.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вы вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. ( . Слайд 2 )
“ Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Будем накачивать и тренировать умственные мышцы. Поэтому повторим основные тригонометрические формулы. ТЕСТ (Слайд 4)(Слайд 5)
Мы повторили формулы, теперь можем помочь двум друзьям, назовём их Ислам и Магомед.
После преобразования некоторого очень сложного тригонометрического выражения А они получили следующие выражения: (Слайд 6)
(Слайд 7) Каждый отстаивал свой ответ. Как узнать кто из них прав? Обратились к Артёму, который дружит с Петром “Платон мне друг, но истина дороже”: сказал Артём и предложил несколько способов разрешения их спора. А какие вы можете предложить способы установить истину? Предлагают способы установления истины (Слайд 8):
1) Преобразовать, упростить А П и А с , т.е. привели к одному выражению
2) А П – А с = 0
3) …..
Т. е. оба были правы. И их ответы равны при всех допустимых значениях α и β .
Как называются такие выражения? Тождествами. Какие тождества вы знаете?
Тождество , основное понятие логики, философии и математики; используется в языках научной теорий для формулировки определяющих соотношений, законов и теорем.
Тождество – философская категория, выражающая равенство, одинаковость предмета, явления самим с собой или равенство нескольких предметов.
В математике тождество – это равенство, которое справедливо для любых допустимых значений входящих в него переменных. (Слайд 9)
Тема урока : “Тригонометрические тождества”.
Цели: найти способы.
Двое работают у доски.
№ 2. Доказать тождество.

П.ч.=Л.ч.
Тождество доказано.
№ 3. Доказать тождество:

1 способ:

2 способ:
Способы доказательства тождеств.
правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным.
Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным.
Из правой части тождества вычитаем левую часть.
Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Для чего необходимо уметь доказывать тригонометрические тождества? В ЕГЭ задание С1 тригонометрические уравнения!
Решается № 465-467
Итак, подведем итоги урока. (Слайд 10)
Какова была тема урока?
Какие способы доказательства тождеств вам известны?
1. Преобразование левой части к правой или правой к левой.
2. Преобразование левой и правой части к одному и тому же выражению.
3. Составление разности левой и правой частей и доказательство равенства этой разности нулю.
Какие формулы при этом используются?
1. Формулы сокращенного умножения.
2. 6 тригонометрических тождеств.
Рефлексия урока. (Слайд 11)
Продолжите фразы:
– сегодня на уроке я узнал …
– сегодня на уроке я научился…
– сегодня на уроке я повторил…
– сегодня на уроке я познакомился…
– сегодня на уроке мне понравилось…
Домашнее задание. №№465-467 (Слайд 12)
Творческое задание: Подготовить презентацию о знаменитых тождествах математики. (Например тождество Эйлера.) (Слайд
Класс: 10
“Математическая истина, независимо
от того, в Париже или в Тулузе, одна и та же”
Б. Паскаль
Тип урока: Урок формирования умений и навыков.
Урок общеметодологической направленности.
Деятельностная цель: формирование способности учащихся к новому способу действия, связанному с построением структуры изученных понятий и алгоритмов.
Цели урока:
- дидактическая: научить применять полученные ранее знания, умения и навыки для упрощения выражений и доказательства тригонометрических тождеств.
- развивающая: развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи, вырабатывать умение анализировать и сравнивать.
- воспитательная: показать, что математические понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи, продолжить формирование эстетических навыков при оформлении записей, навыков контроля и самоконтроля.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sinα, cosα, tgα, ctgα,соотношение sin 2 α+ cos 2 α =1 и т.д.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вы вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. (Презентация . Слайд 2 )
“Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Будем накачивать и тренировать умственные мышцы. Поэтому повторим основные тригонометрические формулы. (Слайд 3)
(Слайд 4)

(Слайд 5)
Мы повторили формулы, теперь можем помочь двум друзьям, назовём их Пётр и Степан.
После преобразования некоторого очень сложного тригонометрического выражения А они получили следующие выражения: (Слайд 6)

(Слайд 7) Каждый отстаивал свой ответ. Как узнать кто из них прав? Обратились к Артёму, который дружит с Петром “Платон мне друг, но истина дороже”: сказал Артём и предложил несколько способов разрешения их спора. А какие вы можете предложить способы установить истину? Предлагают способы установления истины (Слайд 8):
1) Преобразовать, упростить А П и А с, т.е. привели к одному выражению
2) А П – А с = 0
Т. е. оба были правы. И их ответы равны при всех допустимых значениях α и β .
Как называются такие выражения? Тождествами. Какие тождества вы знаете?
То ждество , основное понятие логики, философии и математики; используется в языках научной теорий для формулировки определяющих соотношений, законов и теорем.
В математике тождество – это равенство, которое справедливо для любых допустимых значений входящих в него переменных. (Слайд 9)
Тема урока: “Тригонометрические тождества”.
Цели: найти способы.
Двое работают у доски.
№ 2. Доказать тождество.

Тождество доказано.
№ 3. Доказать тождество:

1 способ:

2 способ:
Способы доказательства тождеств.
- правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным.
- Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным.
- Из правой части тождества вычитаем левую часть.
- Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Для чего необходимо уметь доказывать тригонометрические тождества? В ЕГЭ задание С1 тригонометрические уравнения!
Решается № 87 (п. 3)
Итак, подведем итоги урока. (Слайд 10)
Какова была тема урока?
Какие способы доказательства тождеств вам известны?
1. Преобразование левой части к правой или правой к левой.
2. Преобразование левой и правой части к одному и тому же выражению.
3. Составление разности левой и правой частей и доказательство равенства этой
разности нулю.
Какие формулы при этом используются?
1. Формулы сокращенного умножения.
2. 6 тригонометрических тождеств.
Рефлексия урока. (Слайд 11)
Продолжите фразы:
– сегодня на уроке я узнал …
– сегодня на уроке я научился…
– сегодня на уроке я повторил…
– сегодня на уроке я познакомился…
– сегодня на уроке мне понравилось…
Домашнее задание. Глава VIII; §6; № 78(четные); № 80(2; 4); № 87(2; 4). (Слайд 12)
Творческое задание: Подготовить презентацию о знаменитых тождествах математики. (Например тождество Эйлера.) (Слайд 13)
Пример 2. Доказать тождество
Это тождество мы будем доказывать путем преобразования выражения, стоящего в правой части.
Способ 1.

Поэтому 
Способ 2.
Прежде всего заметим, что ctg α =/= 0; в противном случае не имело бы смысла выражение tg α = 1 / ctg α . Но если ctg α =/= 0, то числитель и знаменатель подкоренного выражения можно умножить на ctg α , не изменяя значения дроби. Следовательно,

Используя тождества tg α ctg α = 1 и 1+ ctg 2 α = cosec 2 α , получаем
Поэтому  что и требовалось доказать.
что и требовалось доказать.
Замечание. Следует обратить внимание на то, что левая часть доказанного тождества (sin α ) определена при всех значениях α , а правая - лишь при α =/= π / 2 n.
Поэтому только при всех допустимых значениях α Вообще же эти выражения не эквивалентны друг другу.
Пример 3. Доказать тождество
sin (3 / 2 π + α ) + cos (π - α ) = cos (2π + α ) - 3sin ( π / 2 - α )
Преобразуем левую и правую части этого тождества, используя формулы приведения:
sin (3 / 2 π + α ) + cos (π - α ) = - cos α - cos α = - 2 cos α ;
cos (2π + α ) - 3sin ( π / 2 - α ) = cos α - 3 cos α = - 2 cos α .
Итак, выражения, стоящие в обеих частях данного тождества, приведены к одному и тому же виду. Тем самым тождество доказано.
Пример 4. Доказать тождество
sin 4 α + cos 4 α - 1 = - 2 sin 2 α cos 2 α .
Покажем, что разность между левой и правой частями. данного тождества равна нулю.
(sin 4 α + cos 4 α - 1) - (- 2 sin 2 α cos 2 α ) = (sin 4 α + 2sin 2 α cos 2 α + cos 4 α ) - 1 =
= (sin 2 α + cos 2 α ) 2 - 1 = 1 - 1 = 0.
Тем самым тождество доказано.
Пример 5. Доказать тождество

Это тождество можно рассматривать как пропорцию. Но чтобы доказать справедливость пропорции a / b = c / d , достаточно показать, что произведение ее крайних членов ad равно произведению ее средних членов bc . Так мы поступим и в данном случае. Покажем, что (1 - sin α ) (1+ sin α ) = cos α cos α .
Действительно, (1 - sin α ) (1 + sin α ) = 1 -sin 2 α = cos 2 α .








 Уравнения онлайн Реши уравнение х 4
Уравнения онлайн Реши уравнение х 4 Экономика. Спрос и предложение. Равновесная цена Спрос больше предложения то на рынке
Экономика. Спрос и предложение. Равновесная цена Спрос больше предложения то на рынке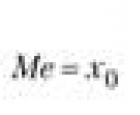 Децильный коэффициент дифференциации доходов населения
Децильный коэффициент дифференциации доходов населения Тригонометрические тождества примеры доказательства
Тригонометрические тождества примеры доказательства